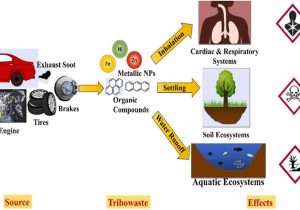
به گزارش پایگاه خبری کلام قلم، مبحث ریاضیات فازی، عملا ریاضیات کلاسیک را به چالش کشید و به همین دلیل در ابتدا، مخالفتهای زیادی با آن شد. همانطور که میدانیم، در منطق کلاسیکی یا منطق ارسطویی یا منطق باینری و یا منطق دیجیتالی، هر گزاره منطقی تنها میتواند دو حالت (صفر یا یک) اختیار کند؛ […]
به گزارش پایگاه خبری کلام قلم، مبحث ریاضیات فازی، عملا ریاضیات کلاسیک را به چالش کشید و به همین دلیل در ابتدا، مخالفتهای زیادی با آن شد. همانطور که میدانیم، در منطق کلاسیکی یا منطق ارسطویی یا منطق باینری و یا منطق دیجیتالی، هر گزاره منطقی تنها میتواند دو حالت (صفر یا یک) اختیار کند؛ هر گزاره یا درست است و یا نادرست (True | False) و حالت دیگری وجود ندارد؛ بهعنوان مثال، یا روز است یا شب؛ عدد یا عضو مجموعهای هست یا نیست، یا سفید است یا سیاه، یا قد بلند است یا قد کوتاه، یا لاغر است یا چاق، یا باز است یا بسته، یا سرد است یا گرم، یا دختر است یا پسر، یا چپ یا راست، یا بالا یا پایین و …؛ لیکن در منطق فازی هر گزاره میتواند درصدی درست و درصدی نادرست (بین صفر و یک) باشد؛ در منطق فازی، صرفا دو حالت برای گزاره، قابل اختیار نیست و گزاره میتواند بهصورت پیوسته، همزمان درصدی درست و درصدی نادرست (بین صفر و یک و نه الزاما خود صفر یا یک) باشد؛ در حقیقت، منطق فازی، دنیا را صرفا به رنگ سیاه یا سفید نمیبیند و میگوید که بین سیاه و سفید، بیشمار رنگ، از جمله خاکستری نیز وجود دارد؛ بحث سطح خاکستری و طوسی، در سیستمهای فازی، همین موضوع است؛ با تفاسیر فوق، میتوان گفت که مجموعههای کلاسیک، حالت خاصی از مجموعههای فازی هستند.
اگر حرف یونانی میو، بیانگر میزان تعلق عضوی به مجموعهای (مثلا A) باشد، برای مجموعههای کلاسیک، این مقدار صرفا ۰ یا ۱ است؛ در صورتی که برای مجموعههای فازی میتواند سایر مقادیرِ بین ۰ و ۱ را نیز اختیار کند.
بهعلت تفاوت مقدار عضویت در بین مجموعههای دقیق با مجموعههای فازی، میتوان گفت که مجموعههای کلاسیک، حالت خاصی از مجموعههای فازی هستند؛ یا بهعبارتی مجموعههای فازی بر اثر توسعه و بسط مجموعههای کلاسیک بهوجود آمدهاند؛ بهطوری-که مقدار تعلق در آنها میتواند علاوه بر صفر و یک، عددی در بازه [۰ , ۱] باشد.
در واقع، در منطق فازی صرفا ۰ و ۱ (باینری بودن نتیجه گزارهها) مطرح نیست و درستی یا عدم صحت گزاره میتواند عددی بین ۰ و ۱ باشد؛ بهعنوان مثال وقتی فردی بهنام علیرضا محمودیفرد در کلاسِ درسِ منطق فازی و کاربرد آن در مدیریت، مشغول تدریس است و میخواهیم میزان تعلق اعضای کلاس نسبت به مجموعهی افراد در حال یادگیریِ منطق فازی را بسنجیم، در مورد میزان تعلقِ علیرضا محمودیفرد به این مجموعه، چه میتوان گفت؟ ممکن است از نظر فردی، میزان تعلق وی، صفر باشد، چون مدرسِ درس است و در کلاس، نقش استاد را بهعهده دارد نه یادگیرنده؛ ممکن است از نظر فردی دیگر، میزان تعلق وی، یک باشد، چون همزمان با تدریس، به دانش خود او نیز افزوده میشود و یا حداقل تجربهاش در این درس، بیشتر میشود؛ ممکن است هم از نظر فردی دیگر، میزان تعلق او، ۰٫۵ باشد، چون نه دانشجو است که صرفا نقش یادگیرنده را داشته باشد (مقدار تعلقِ یک) و نه مسلط به تمام مفاهیم این شاخهی علمی است که نیازی به توسعهی فردی در این شاخه نداشته باشد و لازم نباشد چیزی به دانشش افزوده شود (تعلق صفر)؛ به هر حال، نظرات افراد مختلف در مورد مقدار عضویت، میتواند متفاوت باشد و چنین موضوعی، از ویژگیهای منطق فازی است؛ اینکه هرکس ممکن است نظری متفاوت داشته باشد و طراحِ آگاه و مجرب است که تصمیم میگیرد چگونه توابع عضویت و قوانین را تدوین کند.
همچنین بحث دیگر، نسبت و نسبی بودن منطق فازی است؛ علیرضا محمودیفرد با قدِ معادل ۱۸۰سانتیمتر، قدبلند محسوب میشود یا قدکوتاه؟ ممکن است از نظر فردی، قدبلند باشد، از نظر فردی دیگر دارای قد متوسط و حتی از نظر فردی، قدکوتاه؛ ممکن است اگر علیرضا محمودیفرد، در ایران، ترکیه، عراق و … حضور داشته باشد، غالبِ افراد، او را بیشتر دارای قد متوسط، تلقی کنند؛ احتمالا اگر علیرضا محمودیفرد در کشورهای سنگاپور، تایوان، تایلند و … باشد، اغلبِ افراد او را قدبلند در نظر بگیرند؛ شاید اگر علیرضا محمودیفرد در کشورهای جمهوی چک، لهستان، صربستان و … باشد، درصد قابل توجهی از افراد، او را دارای قد نه چندان بلند و حتی بعضا کوتاه، عنوان کنند؛ همین مفهوم، از خصوصیات منطقِ فازی است.
در مثالی دیگر میخواهیم به بررسی دمای هوای شهر با استفاده از منطق فازی بپردازیم؛ در گفتار روزمره، از کلمات خاصی همچون داغ، خیلی خیلی گرم، خیلی گرم، گرم، معتدل، خنک، سرد، خیلی سرد، خیلی خیلی سرد، یخبندان و … استفاده میکنیم؛ بهعنوان مثال میگوییم که هوا گرم است، که این گرما، طبیعتا در ذهن ما یک بازه دمایی را در برمیگیرد، اما معمولا در خصوص عدد دما توسط عوام صحبت نمیشود؛ مثلا اگر دما بین ۳۶ تا ۴۰ درجه سلسیوس باشد، گوییم هوا خیلی گرم است، که این ابرازِ احساسِ گرم بودن، با توجه به فرامین مغز و واکنشهای بدن که بهطور خودکار نسبت به شرایط آب و هوایی داده میشود (همچون گرگرفتگی، بالا رفتن فشار خون، بیقراری، تعریق و …)، صورت میگیرد.
در گفتارِ انسانها معمولا عدد دما بیان نمیشود و میزان دما با توجه به همان واکنشها و احساسات بهصورت یک واژه یا عبارت تبیین میشود؛ مثلا گفته نمیشود که دمای هوا ۱۲٫۸ درجه سانتیگراد است و این دما، بهصورت “هوا سرد است!” بیان میشود؛ بهعبارت ساده، در منطق فازی، از مفاهیم گفتاری که مفهوم عددی را میرسانند، استفاده میشود و این یعنی محاسبه با کلمات و عبارات توسط دانش انسانی؛ بهعنوان مثال، در گفتگوی انسانی متغیرهای زبانی و کلمههایی همچون بسیار، اندکی، زیاد، کمی، خیلی، تاحدی، نزدیک، تقریبا، نسبتا، خیلی خیلی و … بهکار برده میشوند که منطق فازی نیز مفهومی منطبقبر دانش انسانی داشته و بدینخاطر مزایای زیادی نیز به همراه دارد.
برای مجموعههای فازی هم، عملگرهای مکمل (Com)، اشتراک (T-Norm) و اجتماع (S-Norm) تعریف میشود؛ عملیاتهای منطق ارسطویی (مانند جمع و ضرب)، در منطق فازی هم صادق است؛ بسیاری از قوانین منطق کلاسیک مانند قانون دمورگان، در منطق فازی نیز برقرار است. در کل، بحث ریاضیات فازی گرچه بنیان ریاضیت کلاسیک را به چالش کشید، ولی بهعلت جذابیتهایی که دارد، مخاطبینی نیز برای خود داراست.
به قلم: مهندس علیرضا محمودیفرد-محقق و مدرس دانشگاهها